Bottom-up Object Detection by Grouping Extreme and Center Points

写在前面

本文与2019年1月23日挂在arxiv上，是目前单阶段目标检测性能最好的研究，在COCO测试集上达到了AP43.2%

本文是CornerNet的改进，他们的思想都是将目标检测问题转换为某种形式的关键点提取问题，与流行的目标检测方法都不同

CornerNet是将目标的top-left和bottom-right点作为关键点进行检测

ExtremeNet则是提取了left-most, right-most, top-most, bottom-most四个点，再用纯几何的方法得到最终的目标

主要思想

作者认为，当前长方形的anchor并不是大多数物体真正的形状，强行将所有物体放在同样的anchor中是不合理的，其中会包含很多干扰性的背景像素

相比于CornerNet本文的方法有以下两点的不同：

关键点的选取和组合不同，作者认为，corner只是另一种形式的的bbox，也会遇到大多数top-down目标检测器一样的问题。另外，corner点定义在了物体外部，加大了神经网络的识别难度，所以ExtremeNet选择了在目标上的关键点
CornerNet是以几何式组合的，而本文完全依靠物体外观，没有隐式的特征学习。本文方法的实际表现要好很多。

本文方法的基本结构如下图所示：

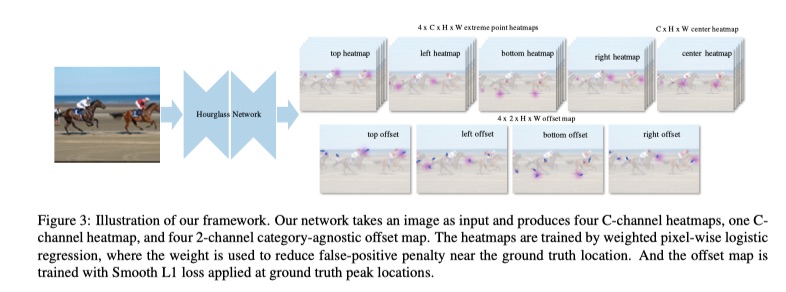
extremenet

ExtremeNet的输出通道数为：\(5*c+4*2\)。对每个类别，预测4张极值点heatmap和1张center map所以是5张。然后，对每种极值点heatmap，再预测2张offset map（分别对应XY轴方向），注意是所有类别公用的且center map没有，所以只有4x2张。

关键点

标注方法

传统标注使用矩形框标注目标，而矩形框一般会用左上角和右下角两个点表示。

而在ExtremeNet中，使用四点标注法，即一个目标用上下左右四个方向上的极值点来表示。额外的，通过这四个点可以计算出该目标的中心坐标。
关键点检测

使用fully convolutional encoder-decoder network预测一个多通道heatmap，每个通道都对应一个类别的关键点。

使用HourglassNetwork作为backbone，对每张heatmap进行加权逐点逻辑回归，加权的目的是为了减少ground truth周围的虚警惩罚。
中心点分组

大体分为两个步骤：
- 第一步，ExtrectPeak。即提取heatmap中所有的极值点，极值点定义为在3x3滑动窗口中的极大值。
- 第二步，暴力枚举。对于每一种极值点组合（进行适当的剪枝以减小遍历规模），计算它们的中心点，如果center map对应位置上的响应超过预设阈值，则将这一组5个点作为一个备选，该备选组合的score为5个对应点的score平均值。
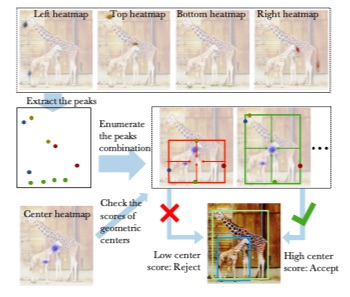
1. Ghost box抑制
  
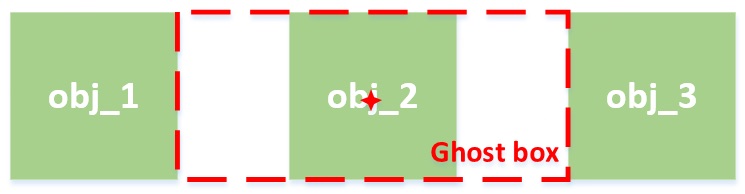
  何为ghost box？如下图所示，若存在多个并排排列且大小相近的物体，则对obj_2这个目标来说，在指定center时，会有两个选择，一个是真实的目标，另一个是大一圈的ghost box
2. 边缘融合
  
  极值点的定义并不唯一，这就导致如果物体沿着水平或垂直方向边缘形成极值点的话（比如汽车顶部），沿着该边缘的点可能都会被当做极值点。网络会对沿对象任何对齐的边缘产生弱响应，而不是单个的强响应。这会引起两个问题：一方面，较弱的响应可能低于预设的极值点阈值，导致漏掉所有的点；另一方面，即使侥幸超过了阈值，但其score可能还是PK不过轻微旋转过的目标相比（在两个方向上都有较大的响应）。
  
  解决办法是，对每一个极值点，向它的两个方向进行聚集。具体做法是，沿着X/Y轴方向，将第一个单调下降区间内的点的score按一定权重累加到原极值点上。效果如下图所示，可以看出，红圈部分的响应明显增强了。