DARTS - 白一帆的博客

DARTS – Differentiable Architecture Search

1. 搜索空间

1.1 搜索空间定义

DARTS搜索的是单个计算单元(cell)，也就是一个小型网络。然后将多个cell相连组成一个大网络。超参数layers表示有多少个cell相连，如果layers=8，就表示网络由8个cell前后相连组成 DARTS首先定义了cell的基本结构，它由2个输入节点、1个输出节点、若干个中间节点和若干条边组成：

输入节点：对CNN而言，两个输入节点分别是前两层的输出；对RNN而言，输入节点分别是当前时刻的输入和上一时刻的状态
输出节点：输出节点由每一个中间节点concat而来
中间节点：中间节点由它的前继通过边计算再求和得到，如以下公式所示，其中\(x^{(i)}\)表示第i个节点，\(o^{(i,j)}\)表示第i个节点到第j个节点之间的边 \(x^{(j)}=\sum_{i<j}o^{(i,j)}(x^{(i)})\tag{1}\)
边：边代表的是不同的operation（例如3x3 conv），在搜索的过程中，所有边都会存在并参与训练，最后加权平均。训练的就是各个operation的权重值，期望的结果是效果越好的边权值越大。特别的，\(o^{(i,j)}\)可以为0，表示两个节点之间没有连接关系

1.2 Darts使用的搜索空间：

Normal

separable conv	dilated conv	max pooling	average pooling	identity	zero
3x3, 5x5	3x3, 5x5	3x3	3x3	1	1

Operation:

以上所有操作(operation)的stride均为1，同时还有padding操作
采用了ReLU-Conv-BN的卷积操作顺序，每一个separable conv均采用两次这样的顺序结构

Cell:

每个cell包含7个节点
第k个cell的第一个输入对应于第k-2个cell的输出，第k个cell的第二个输入对应于第k-1个cell的输出

Reduction

Reduction cell位于网络总深度的\(\frac13\)和\(\frac23\)处，在Reduction cell中，所有的靠近输入节点的运算的stride均设为2

2. 连续化方法

首先将多种operation（conv, maxpooling, zero等）定义为集合\(O\)，为了使搜索空间连续化，DARTS将特定operation的分类选择松弛化为全部可能operation的softmax结果： \(\overline o^{(i,j)}(x)=\sum_{o\in O}\frac{exp(\alpha_o^{(i,j)})}{\sum_{o'\in O}exp(\alpha_{o'}^{(i,j)})}o(x)\tag{2}\) 其中，\(\alpha^{(i,j)}\)表示边\(o^{(i,j)}\)的operation混合权重，可以表示为一个维度为\(|O|\)的权重，搜索过程学习的就是边的混合权重。搜索最后，Darts将最有可能的operation代替混合operation(即\(\overline o\))，最后得到一个离散的结构： \(o^{(i,j)}=argmax_{o\in O}\ \alpha_o^{(i,j)}\tag{3}\)

首先不知道各个节点之间的边的连接方式
在两两节点之间部署所有的混合operation边
将其归类为一个双层优化问题，交替优化混合operation权重\(\alpha\)和网络参数\(\omega\)
得到离散化的最终结构

DARTS引入了双层优化问题(bilevel optimization problem)来解决\(\alpha\)和\(\omega\)的同时优化，其中网络结构\(\alpha\)为上层变量，网络参数\({\omega}\)为下层变量， \(\begin{eqnarray*} &&\min_{\alpha} L_{val}(\omega^*(\alpha), \alpha)\tag{4} \\ &&s.t. \omega^*(\alpha) = \mathop{\arg\min}_wL_{train}(\omega, \alpha)\tag{5} \end{eqnarray*}\)

3. 搜索策略

3.1 前提

使用DARTS搜索策略的前提：

连续的网络结构搜索空间\(\alpha\)
对\(\alpha\)可微的loss

3.2 目标函数

3.2.1 优化问题定义

我们要搜索的目标有两部分组成：

模型网络结构：\(\alpha\)
模型权重：\(\omega\)

我们的目标是找到一组最好的\(\alpha\)和\(\omega\)，考虑到\(\alpha\)和\(\omega\)之间的相关性我们每更新一次公式\((4)\)中的\(\alpha\), 就要用新的\(\alpha\)通过公式\((5)\)计算出新的\(\omega^*\), 对于这种嵌套优化问题，我们可以通过梯度下降的策略交替优化\(\alpha\)和\(\omega\)。

3.2.2 目标函数定义

因为要对\(\alpha\)和\(\omega\)交替优化，所以我们需要为其分别设计目标函数。

\(\omega\)对应的目标函数如下：

\[L_{train}(\omega, \alpha) \tag{6}\]

给定\(\alpha\), 我们通过训练数据集上的loss评估\(\omega\).

\(\alpha\)对应的目标函数如下：

\[L_{val}(\omega - \xi \nabla_\omega L_{train}(\omega, \alpha), \alpha) \tag{7}\]

给定\(\omega\), 我们评估\(\alpha\)的方式是，先让\(\omega\)在当前\(\alpha\)和训练集上优化一步，然后再计算更新后的\(\omega\)和当前\(\alpha\)在测试数据集上的loss.

3.2.3 优化步骤

循环交替执行以下步骤，直到loss收敛：

第一步：根据公式\((6)\)用梯度下降法更新\(\omega\)
第二步：根据公式\((7)\)用梯度下降法更新\(\alpha\)

以上每一步需要向对应的目标函数求导，其中，公式\((7)\)的求导比较复杂，我们重点分析一下。

3.2.4 求导

\[L = L_{val}(\omega - \xi \nabla_{\omega} L_{train}(\omega, \alpha), \alpha) \tag{8}\]

令：

\[\omega^{'} = \omega - \xi \nabla_{\omega} L_{train}(\omega, \alpha) \tag{9}\]

推导如下：

\[\begin{eqnarray*} \nabla_{\alpha}{L} &&= \nabla_{\alpha}L_{val}(\omega^{'}, \alpha) * \nabla_{\alpha}({\alpha}) + \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha) * \nabla_{\alpha}(\omega - \xi \nabla_\omega L_{train}(\omega, \alpha)) \\ &&= \nabla_{\alpha}L_{val}(\omega^{'}, \alpha) + \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha) * \nabla_{\alpha}(\omega - \xi \nabla_\omega L_{train}(\omega, \alpha)) \\ &&= \nabla_{\alpha}L_{val}(\omega^{'}, \alpha) - \xi \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha) * \nabla^2_{\omega, \alpha} L_{train}(\omega, \alpha) \tag{10}\\ \end{eqnarray*}\]

在等式\((10)\)中，第二项直接计算比较困难，对其进行近似模拟，

令：

\[\Delta \omega = \epsilon \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha)\]

\(\epsilon\)为一个很小的标量，令\(\epsilon=\frac{0.01}{\|\|\nabla_{\omega' }L_{val}(\omega',\alpha)\|\|_2}\)

则：

\[\begin{eqnarray*} \nabla^2_{\omega, \alpha} L_{train}(\omega, \alpha) &&\approx \frac { \nabla_{\alpha} L_{train}(\omega + \Delta \omega, \alpha) - \nabla_{\alpha} L_{train}(\omega - \Delta \omega, \alpha)}{2\Delta \omega} \tag{11} \end{eqnarray*}\]

所以：

\[\begin{eqnarray*} &&\nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha) * \nabla^2_{\omega, \alpha} L_{train}(\omega, \alpha) \\ &&\approx \frac { \nabla_{\alpha} L_{train}(\omega +\epsilon \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha), \alpha) - \nabla_{\alpha} L_{train}(\omega - \epsilon \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha), \alpha)}{2\epsilon} \tag{12} \end{eqnarray*}\]

综上，等式\((10)\)可写为：

\[\begin{eqnarray*} \nabla_{\alpha}{L} &&= \nabla_{\alpha}L_{val}(\omega^{'}, \alpha) - \xi \frac { \nabla_{\alpha} L_{train}(\omega +\epsilon \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha), \alpha) - \nabla_{\alpha} L_{train}(\omega - \epsilon \nabla_{\omega^{'}} L_{val}(\omega^{'}, \alpha), \alpha)}{2\epsilon} \tag{13}\\ \end{eqnarray*}\]

一阶近似：当\(\xi=0\)，等式\((10)\)的后半部分为0，DARTS认为是原式的一阶近似
二阶近似：当\(\xi>0\)，认为是二阶近似论文经过实验证明，二阶近似的收敛效果更好，但是效率稍逊

3.3 计算步骤

设当前模型权重参数为\(\omega_{k-1}\), 网络结构参数为\(a_{k-1}\)

第一步更新model parameters

从train数据集读取一个batch的数据，按以下公式更新模型权重参数： \(\omega_k = \omega_{k-1} - \xi \nabla_{\omega}L_{train}(\omega_{k-1}, \alpha_{k-1}) \tag{14}\) 其中\(\xi\)是学习率 \(\alpha\)和\(\omega\)的联合优化问题构成了一个Stackelberg博弈问题，由\(\alpha\) optimizer(leader)和\(\omega\) optimizer(follower)组成

第二步 compute unrolled step

计算\(\omega^{'}\), 在pytorch和tensorflow的实现中，这一步叫unrolled step，这一步骤代替了公式\((5)\)中\(\omega^*(\alpha)\)的计算首先构建一个与model一样的unrolled_model，然后将\(\omega'\)的值保存在unrolled_model上 \(\omega^{'} = \omega_k - \xi \nabla_\omega L_{train}(\omega_k, \alpha_{k-1}) \tag{15}\) 至此，公式\((4)(5)\)简化为公式\((8)\)，进而可以得到unrolled_model_loss: \(L_{val}(\omega ', \alpha)\)

第三步更新arch parameters

根据公式\((13)\)可知\(\nabla_\alpha L\)的计算可以拆分为三个部分:\(\nabla_{\alpha}L_{val}(\omega',\alpha), \nabla_{\alpha}L_{train}(\omega+\Delta\omega,\alpha), \nabla_{\alpha}L_{train}(\omega-\Delta\omega,\alpha)\)

其中\(\nabla_{\alpha}L_{val}(\omega',\alpha)\)由unrolled_model_loss对\(\alpha\)求导得到后两项先求在model上的loss: \(L_{train}\)，再对\(\alpha\)求导可以得到

需要注意的是，tf和pytorch实现中\(\omega \pm \Delta\omega\)的操作是在\(\omega\)上Inplace操作的，所以采用了先\(+\Delta\omega\)再\(-2*\Delta\omega\)，最后再\(+\Delta\omega\)还原的操作

4. 获得离散结构

经过得到连续结构的编码\(\alpha\)后，离散结构通过以下方式得到：

保留每个节点的最有用的k个前继，在CNN中k=2，在RNN中k=1，用下面的公式进行计算 \(max_{o\in O,o\neq zero}\frac{exp(\alpha_o^{(i,j)})}{\sum_{o'\in O}exp(\alpha_{o'}^{(i,j)})}\tag{16}\)
将每个Mixed Operation边替换为其对应的argmax operation

5. 实验结果

5.1 CIFAR10

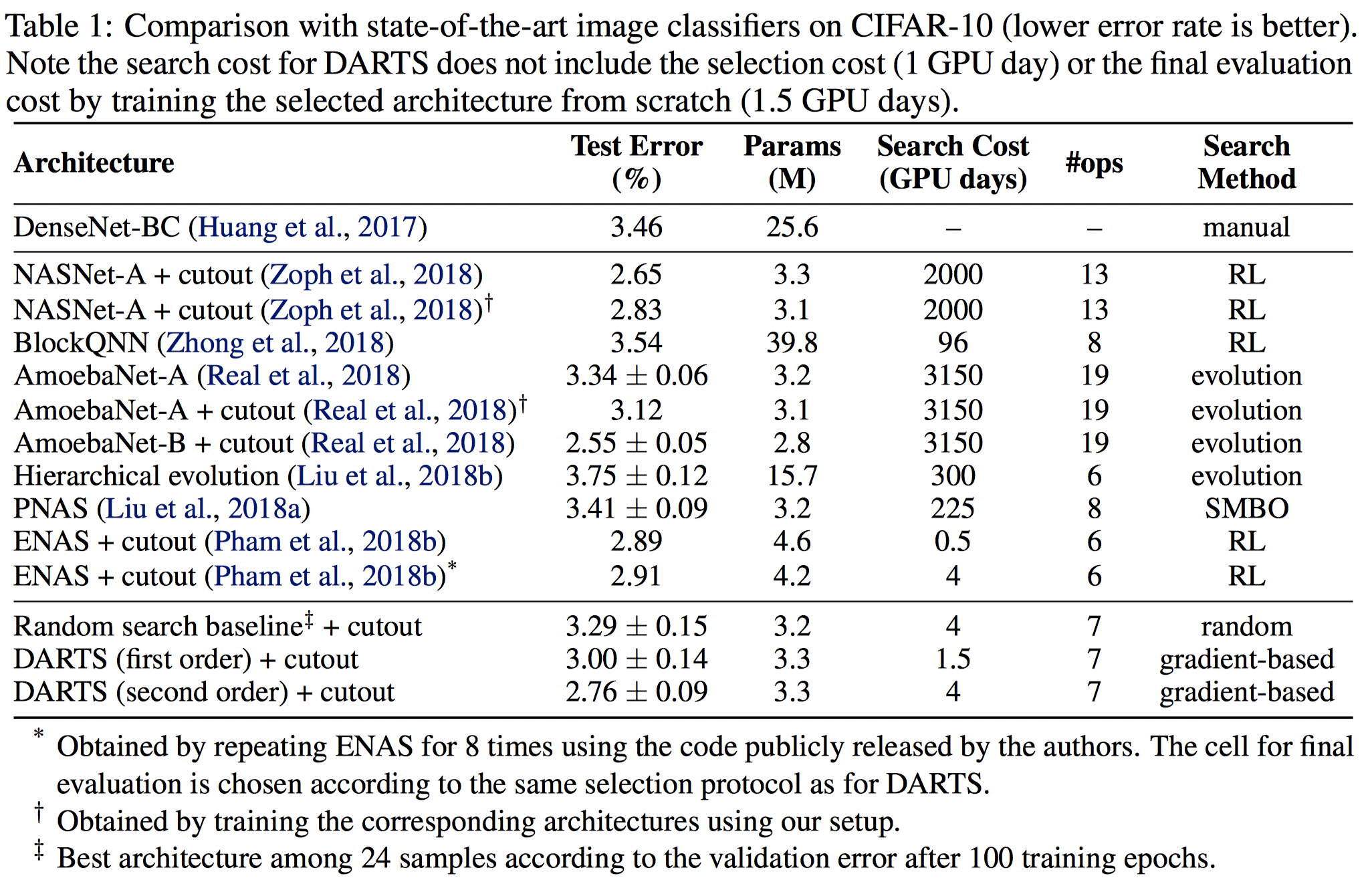
darts-cifar10

5.3 PTB

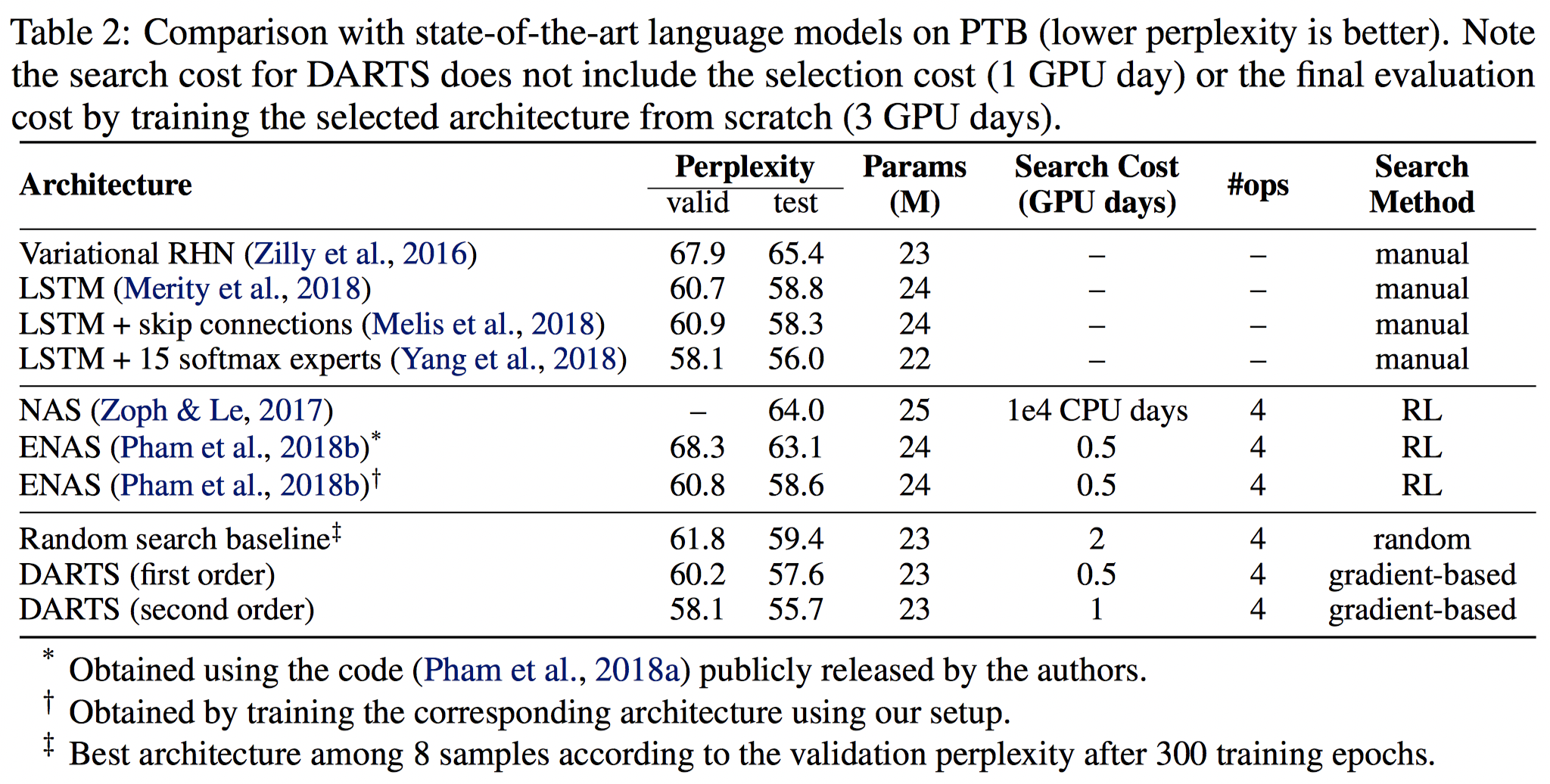
darts-ptb

5.3 ImageNet

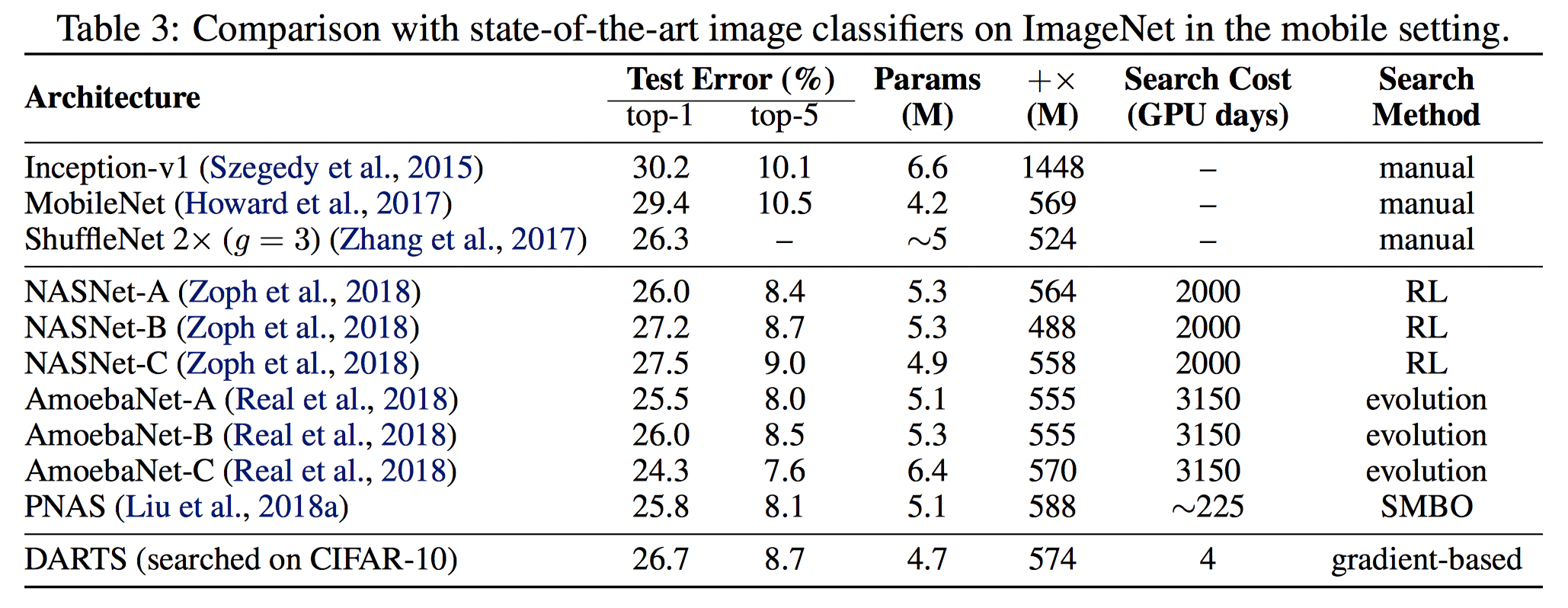
darts-imagenet

6. 实现分析

6.1 pytorch实现分析

https://github.com/quark0/darts

6.1.1 train_search.py

程序模型搜索的主要接口文件，包含了darts搜索的基本逻辑：loss、学习率、优化器、数据等，主要包含main(), train(), infer()三个函数

a. main()

以50个epoch交替进行train()和infer()

Loss	cross_entropy
\(\omega\) Optimizer	sgd+momentum
\(\alpha\) Optimizer	Adam
Data	0.5 portion for train(\(\omega\))（preprocessed）, 0.5 portion for valid(\(\alpha\))
LR strategy	CosineAnnealingLR

b. train()

train逻辑主要有三个指标：objs, top1, top5. 分别表示loss, top1/top5准确率

train_search.py代码中L147-155是论文中交叉梯度下降的主逻辑实现， https://github.com/quark0/darts/blob/f276dd346a09ae3160f8e3aca5c7b193fda1da37/cnn/train_search.py#L147-L155

architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled) # arch_param optimize
optimizer.zero_grad()
logits = model(input)
loss = criterion(logits, target)
loss.backward()
nn.utils.clip_grad_norm(model.parameters(), args.grad_clip)
optimizer.step() # model_param optimize

c. infer()

infer逻辑，指标同上对model进行前向计算，根据计算结果得到top1/top5指标和loss

6.1.2. model_search.py

实现了Network/Cell/MixedOp三个类

a. Class Network

表示整个网络模型，其由多个Cell级联组成，其中Cell分为两类: normal和reduction，在\(\frac13\)和\(\frac23\)layer处的cell是reduction cell，见model_search.pyL78-90 L119-128 https://github.com/quark0/darts/blob/f276dd346a09ae3160f8e3aca5c7b193fda1da37/cnn/model_search.py#L78-L90

C_prev_prev, C_prev, C_curr = C_curr, C_curr, C
self.cells = nn.ModuleList()
reduction_prev = False
for i in range(layers):
    if i in [layers//3, 2*layers//3]:
      C_curr *= 2
      reduction = True
    else:
      reduction = False
cell = Cell(steps, multiplier, C_prev_prev, C_prev, C_curr, reduction, reduction_prev)
reduction_prev = reduction
self.cells += [cell]
C_prev_prev, C_prev = C_prev, multiplier*C_curr

https://github.com/quark0/darts/blob/f276dd346a09ae3160f8e3aca5c7b193fda1da37/cnn/model_search.py#L119-L128

def _initialize_alphas(self):
    k = sum(1 for i in range(self._steps) for n in range(2+i))
    num_ops = len(PRIMITIVES)

    self.alphas_normal = Variable(1e-3*torch.randn(k, num_ops).cuda(), requires_grad=True)
    self.alphas_reduce = Variable(1e-3*torch.randn(k, num_ops).cuda(), requires_grad=True)
    self._arch_parameters = [
        self.alphas_normal,
        self.alphas_reduce,
    ]

搜索结果根据第4节的方法获得离散结构，由weights矩阵求最大值得到各个节点的连接关系和各边的运算operation，见model_search.py L135-152 https://github.com/quark0/darts/blob/f276dd346a09ae3160f8e3aca5c7b193fda1da37/cnn/model_search.py#L135-L152

def _parse(weights): # weights[2+3+4+5][len(PRIMITIVES)]
  gene = []
  n = 2
  start = 0
  for i in range(self._steps):
      end = start + n
      W = weights[start:end].copy()
      edges = sorted(range(i + 2), key=lambda x: -max(W[x][k] for k in range(len(W[x])) if k != PRIMITIVES.index('none')))[:2]
      for j in edges:
        k_best = None
        for k in range(len(W[j])):
          if k != PRIMITIVES.index('none'):
            if k_best is None or W[j][k] > W[j][k_best]:
              k_best = k
        gene.append((PRIMITIVES[k_best], j))
      start = end
      n += 1
    return gene

b. Class Cell

cell是网络结构\(\alpha\)搜索的基本单位，分为normal和reduction两类，在一个cell内，输出节点将各个中间节点的结果concat到一起，得到cell的输出，model_search.py L47-58 https://github.com/quark0/darts/blob/f276dd346a09ae3160f8e3aca5c7b193fda1da37/cnn/model_search.py#L47-L58

def forward(self, s0, s1, weights):
    s0 = self.preprocess0(s0)
    s1 = self.preprocess1(s1)

    states = [s0, s1]
    offset = 0
    for i in range(self._steps):
        s = sum(self._ops[offset+j](h, weights[offset+j]) for j, h in enumerate(states))
        offset += len(states)
        states.append(s)
        
    return torch.cat(states[-self._multiplier:], dim=1)

self._ops表示的（2+3+4+5）共14个MixedOp。 (2+3+4+5)的意思是，对第一个中间节点，有2个可能的前继；第二个中间节点，有3个可能的前继；依次类推，对第四个中间节点，有5个可能的前继。所以，共有14个可能的连接关系 L54中weights是一个长度为14的list，前2个元素对应第一个中间节点2个输入的权重，第3-5表示第二个中间节点的3个输入的权重，依次类推。

c. Class MixedOp

MixedOp用来处理两节点之间多种op的计算，将PRIMITIVES中定义的运算都连接上，最后将全部计算加权求和的结果输出, model_search.py L12-22 https://github.com/quark0/darts/blob/f276dd346a09ae3160f8e3aca5c7b193fda1da37/cnn/model_search.py#L12-L22

def __init__(self, C, stride):
    super(MixedOp, self).__init__()
    self._ops = nn.ModuleList()
    for primitive in PRIMITIVES:
        op = OPS[primitive](C, stride, False)
        if 'pool' in primitive:
          op = nn.Sequential(op, nn.BatchNorm2d(C, affine=False))
        self._ops.append(op)

def forward(self, x, weights):
    return sum(w * op(x) for w, op in zip(weights, self._ops))

6.1.3. architect.py

包含一个类：Class Architect，实现了\(\alpha\)参数搜索的相关逻辑对\(\alpha\)参数用Adam优化器对进行了梯度下降优化，即各个节点之间不同运算的权重参数 \(\alpha\)定义于model_search.py L119-128，分为normal和reduce两种情况

在unrolled模式下，类内各函数的执行顺序是step()->_backward_step_unrolled()->compute_unrolled_model()->_construct_model_from_theta()->_hessian_vector_product() step() # 搜索逻辑入口，依次完成\(\alpha\)参数和\(\omega\)参数的更新 backward_step_unrolled() # unroll 近似计算，实现3.3节计算逻辑 compute_unrolled_model() # 完成公式(9)的计算，并将其保存在新的unrolled_model _construct_model_from_theta() # 构建unrolled_model _hessian_vector_product() # 完成公式(13)的有限差分近似计算

6.1.4. genotypes.py

定义了全部边（MixedOp）的操作PRIMITIVES和几种不同的Genotype Genotype描述的是边的连接关系，例如下面的genotype描述的连接关系如图所示： normal=[('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 0), ('sep_conv_3x3', 1), ('sep_conv_3x3', 1), ('skip_connect', 0), ('skip_connect', 0), ('dil_conv_3x3', 2)], normal_concat=[2, 3, 4, 5] 以2个元素为一组，依次映射到上图中的一个蓝色的中间节点

('sep_conv_3x3', 0), ('sep_conv_3x3', 1) # 中间节点0
('sep_conv_3x3', 0), ('sep_conv_3x3', 1) # 中间节点1
('sep_conv_3x3', 1), ('skip_connect', 0) # 中间节点2
('skip_connect', 0), ('dil_conv_3x3', 2) # 中间节点3

这里的前半部分sep_conv_3x3/skip_connect/etc...表示运算类型，后半部分0/1/2/...表示输入来源，例如第一行的意思就是中间节点0的两个输入分别来源于0号节点经过sep_conv_3x3和1号节点经过sep_conv_3x3 最后normal_concat=[2, 3, 4, 5]表示当前normal cell的输出节点是由2-5中间节点的输出(图中蓝色的0-3节点)concat得到的 Genotype后半部分的reduce和normal原理相同，在此不再赘述

6.2 tensorflow实现分析

https://github.com/NeroLoh/darts-tensorflow

6.2.1train_search.py

a. main()

Data, LR strategy, Loss等的实现与Pytroch版本大致相同

因网络包含\(\alpha\)和\(\omega\)两部分参数，所以TF版本定义了两个优化器：leader_opt和follower_opt: leader_opt是网络结构参数\(\alpha\)的优化器， follower_opt是常规权重参数\(\omega\)的优化器 follower_opt依赖于leader_opt，通过tf.control_dependencies实现

训练逻辑部分：以50个epoch交替进行train和infer train逻辑：sess.run([follower_opt，train_loss, accuracy, lr, global_step]) 在每个epoch结束时调用get_genotype()打印当前获得的Genotype, 获得Genotype的方法与本文第4节描述相同 infer逻辑：sess.run([valid_accuracy])

b. compute_unrolled_step()

实现了Pytorch版本的architect.py中的功能，完成Darts一轮搜索逻辑的计算首先得到一个unrolled_model，其\(\omega\)参数直接从model拷贝来 https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/train_search.py#L133-L137

arch_var=utils.get_var(tf.trainable_variables(), 'arch_var')[1]

_,unrolled_train_loss=Model(x_train,y_train,True,args.init_channels,CLASS_NUM,args.layers,name="unrolled_model")
unrolled_w_var=utils.get_var(tf.trainable_variables(), 'unrolled_model')[1]
cpoy_weight_opts=[v_.assign(v) for v_,v in zip(unrolled_w_var,w_var)] # construct unrolled model

进一步可以求得在unrolled_model上的valid loss, 即3.3节的第二步的结果：\(L_{val}(\omega', \alpha)\) https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/train_search.py#L144

_,valid_loss=Model(x_valid,y_valid,True,args.init_channels,CLASS_NUM,args.layers,name="unrolled_model")

再将\(L_{val}(\omega', \alpha)\)对\(\omega'\)求导，得到\(\nabla_{\omega'}L_{val}(\omega',\alpha)\)，进一步可以求得标量\(\epsilon=0.01/||\nabla_{\omega'}L_{val}(\omega',\alpha)||_2\) https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/train_search.py#L147-L151

with tf.control_dependencies([unrolled_optimizer]):
	valid_grads=tf.gradients(valid_loss,unrolled_w_var)

r=1e-2
R = r / tf.global_norm(valid_grads) # epsilon

对于\(\omega\pm\Delta\omega\)的实现，tf是用一步梯度下降来实现的，需要注意的是因为是对\(\omega\) inplace操作的，所以需要先需要按下面的方式计算 https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/train_search.py#L153-L160

# w+ = w + eps*dw'
optimizer_pos=tf.train.GradientDescentOptimizer(R)
optimizer_pos=optimizer_pos.apply_gradients(zip(valid_grads,w_var))
# w- = w+ - 2*eps*dw'
optimizer_neg=tf.train.GradientDescentOptimizer(-2*R)
optimizer_neg=optimizer_neg.apply_gradients(zip(valid_grads,w_var))
# recover w
optimizer_back=tf.train.GradientDescentOptimizer(R)
optimizer_back=optimizer_back.apply_gradients(zip(valid_grads,w_var))

在得到了\(\omega\pm\Delta\omega\)之后就可以根据公式(13)计算\(\alpha\)参数的梯度 TF的用了三层的control_dependencies来保证\(\omega\)相关的计算逻辑。用apply_gradients将最后计算得到的\(\alpha\)相关的梯度更新到\(\alpha\)上 https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/train_search.py#L162-L172

with tf.control_dependencies([optimizer_pos]):
	train_grads_pos=tf.gradients(train_loss,arch_var) # GRAD_train_loss(w+)
	with tf.control_dependencies([optimizer_neg]):
		train_grads_neg=tf.gradients(train_loss,arch_var) # GRAD_train_loss(w-)
		with tf.control_dependencies([optimizer_back]):
			leader_opt= tf.train.AdamOptimizer(args.arch_learning_rate, 0.5, 0.999)
			leader_grads=leader_opt.compute_gradients(valid_loss,var_list =arch_var)
for i,(g,v) in enumerate(leader_grads):
	leader_grads[i]=(g-args.learning_rate*tf.divide(train_grads_pos[i]-train_grads_neg[i],2*R),v) # GRAD_alpha_L

leader_opt=leader_opt.apply_gradients(leader_grads)

c. _pre_process()

对train部分的data进行预处理依次进行padding, random_crop, random_flip_left_right, cutout

6.2.2 model_search.py

实现了MixedOp/Cell/Model/get_genotype等函数

a. MixedOp()

MixedOp表示两两节点之间的运算方式，共有len(PRIMITIVES)种，所有每一个MixOp共有len(PRIMITIVES)个权重参数，这些参数需要配置为tf.AUTO_REUSE https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/model_search.py#L19-L21

with tf.variable_scope(null_scope):
	with tf.variable_scope("arch_var",reuse=tf.AUTO_REUSE):
		weight=tf.get_variable("weight{}_{}".format(2 if reduction else 1,index),[len(PRIMITIVES)],initializer=tf.random_normal_initializer(0,1e-3),regularizer=slim.l2_regularizer(0.0001))

MixedOp将各边全部连接上，并将结果进行加权求和

b. Cell()

Cell逻辑与Pytroch实现相同

c. Model()

实现了网络整体前向逻辑，在layer/3和2*layer/3处使用reduction cell https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/model_search.py#L58-L80

def Model(x,y,is_training,first_C,class_num,layer_num,cells_num=4,multiplier=4,stem_multiplier=3,name="model"):
	with tf.variable_scope(name,reuse=tf.AUTO_REUSE):
		with slim.arg_scope([slim.conv2d,slim.separable_conv2d],activation_fn=None,padding='SAME',biases_initializer=None,weights_regularizer=slim.l2_regularizer(0.0001)):
			with slim.arg_scope([slim.batch_norm],is_training=is_training):
				C_curr = stem_multiplier*first_C
				s0 =slim.conv2d(x,C_curr,[3,3],activation_fn=tflearn.relu)
				s0=slim.batch_norm(s0)
				s1 =slim.conv2d(x,C_curr,[3,3],activation_fn=tflearn.relu)
				s1=slim.batch_norm(s1)
				reduction_prev = False
				for i in range(layer_num):
					if i in [layer_num//3, 2*layer_num//3]:
						C_curr *= 2
						reduction = True
					else:
						reduction = False
					s0,s1 =s1,Cell(s0,s1,cells_num, multiplier, C_curr, reduction, reduction_prev)
					reduction_prev = reduction
				out=tf.reduce_mean(s1, [1, 2], keep_dims=True, name='global_pool')
				logits = slim.conv2d(out, class_num, [1, 1], activation_fn=None,normalizer_fn=None,weights_regularizer=slim.l2_regularizer(0.0001))
				logits = tf.squeeze(logits, [1, 2], name='SpatialSqueeze')
	train_loss=tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits))
	return logits,train_loss

6.2.3 data_utils.py

用read_data()读入cifar10 train data，并按比例将train分为train和valid，train用于常规权重参数\(\omega\)的优化，valid用于网络结构参数\(\alpha\)的优化 https://github.com/NeroLoh/darts-tensorflow/blob/05e6228af144d7d09400a42e21af3e25c1ded862/cnn/data_utils.py#L79-L89

 images["train"], labels["train"] = _read_data(data_path, train_files)

 num_train = len(images["train"])
 indices = list(range(num_train))
 split = int(np.floor(train_portion * num_train))

 images["valid"] = images["train"][split:num_train]
 labels["valid"] = labels["train"][split:num_train]

 images["train"] = images["train"][:split]
 labels["train"] = labels["train"][:split]

1. 搜索空间

1.1 搜索空间定义

1.2 Darts使用的搜索空间：

Normal

Reduction

2. 连续化方法

3. 搜索策略

3.1 前提

3.2 目标函数

3.2.1 优化问题定义

3.2.2 目标函数定义

3.2.3 优化步骤

3.2.4 求导

3.3 计算步骤

第一步 更新model parameters

第二步 compute unrolled step

第三步 更新arch parameters

4. 获得离散结构

5. 实验结果

5.1 CIFAR10

5.3 PTB

5.3 ImageNet

6. 实现分析

6.1 pytorch实现分析

6.1.1 train_search.py

a. main()

b. train()

c. infer()

6.1.2. model_search.py

a. Class Network

b. Class Cell

c. Class MixedOp

6.1.3. architect.py

6.1.4. genotypes.py

6.2 tensorflow实现分析

6.2.1train_search.py

a. main()

b. compute_unrolled_step()

c. _pre_process()

6.2.2 model_search.py

a. MixedOp()

b. Cell()

c. Model()

6.2.3 data_utils.py

CATALOG

FEATURED TAGS

第一步更新model parameters

第三步更新arch parameters