Logistic Regression as a Neural Network
sigmoid
在logistic regression后加一个非线性函数,例如sigmoid()可以使输出满足概率特性
\[0 \leq P_i \leq 1\]
\[\sum{P_i} = 1\]
损失Loss函数$L$
损失函数常用预测值和标签的交叉熵定义:
\[L(\hat{y},y) = -(y * log\hat{y} + (1 - y) * log(1 - \hat{y})) \]
\(y\)代表标签,\(\hat{y}\)代表预测值
##成本Cost函数$J$
成本函数是损失函数$L$的求和取均值,是对整个训练集定义的
\[J(w,b) = \frac{1}{m}\sum_{i=1}^mL(\hat y^{(i)},y^{(i)})\]
梯度下降法
整个神经网络训练的目的就是使成本函数\(J(w,b)\)最小,可以用梯度下降法调整\(w\)和\(b\)满足要求,梯度下降可以定义为下面的形式,通过反复迭代找到最优解
Repeat:{
\[w := w - \alpha\frac{dJ(w,b)}{dw}\]
\[b := b - \alpha\frac{dJ(w,b)}{db}\]
}#\(\alpha\)代表学习率
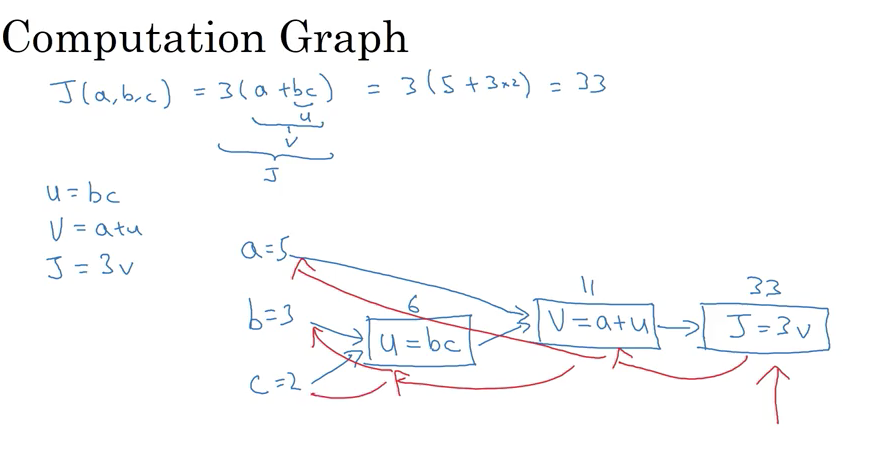
计算图
把一个计算过程用图形的方式表示出来,方便前向计算和反向求导
单层神经网络的梯度下降应用
若神经网络可以定义为:
\[z = w_1x_1 + w_2x_2 +b$——>$a = \sigma(z)$——>$L(a,y)\]
\[\frac{dL}{da} = -\frac{y}{a} + \frac{1-y}{1-a}\]
\[\frac{dL}{dz} = \frac{dL}{da} * \frac{da}{dz} = a - y\]
Python和向量化
基于CPU和GPU都有并行化的SIMD(singal instraction multiply data)指令,如果用python内置函数例如np.dot(),可以充分利用并行性去快速计算
在Python与Numpy编程中需要特别注意变量的维数,例如下面几种定义代表不同的类型
a = np.random.rand(5) #(5,)
b = np.random.rand(5,1) #(5,1)
c = np.random.rand(1,5) #(1.5)
所以十分有必要在代码中用assert语句检验变量的维数,或者reshape()函数改变变量的维度:
c = c.reshape(5,1)
assert(c.shape == (5,1))